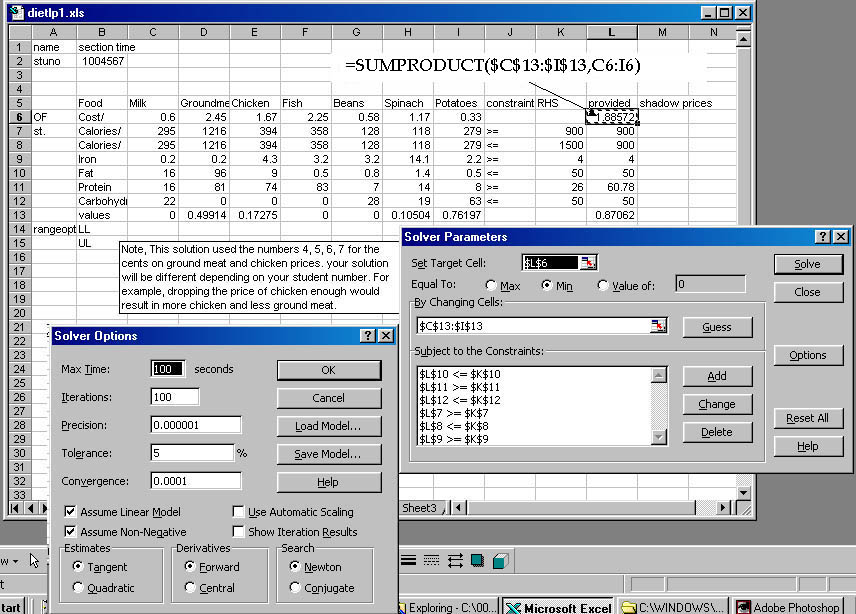
Set this up in EXCEL and solve using Solver
set up the same problem in POM-QM and compare the results.
This comparison should help you interpret the sensitivity and range analyses
from the solver output. Everyone will have slightly different numbers
as you will use the last 4 digits of your student number to replace the
cents in the prices for ground meat and chicken.
Rachel Yang, campus dietitian for a small Illinois college,
is responsible for formulating a nutritious meal plan for students. For
an evening meal, she feels that the following five meal-content requirements
should be met: (1) between 900 and 1,500 calories (you will need two rows
for calories, one to set the upper limit, one to set the lower limit);
(2) at least 4 milligrams of iron; (3) no more than 50 grams of fat; (4)
at least 26 grams of protein; and (5) no more than 50 grams of carbohydrates.
On a particular day, Rachelís food stock includes seven
items that can be prepared and served for supper to meet these requirements.
The cost per pound for each food item and its contribution to each of the
five nutritional requirements are given in the accompanying table:
Use copy, paste special /transpose (video on paste special
transpose) to put the data in a more familiar configuration (columns for
decision variables, rows for objective function and constraints). Duplicate
the calories row to allow two (upper and lower) constraints on calories.
Move the cost coefficients row (objective function) to the top data row.
Add a row for Values (which Solver will manipulate), and rows for Upper
and Lower Limits on the ranges of optimality. Add columns for direction
of constraint, RHS, amount provided, and Shadow Price for each ingredient.

The formula for each 'amount provided' will consist of
the sum of each of the (variable values * amount provided per pound)
The easiest way to do this is through the Sumproduct Function. In cell
L6, enter =sumproduct($C13:$I13,C6:I6) you can do this by entering
"=sumproduct(" then select the ranges, use F4 to absolute references to
the value row and put in the close parenthesis before pushing enter. You
will only have to enter the calculation once, then you can just copy it
down to subsequent rows.
In the event solver tells you there is "no feasible solution
found" check your formulas and make sure you have the right directionality
on the constraints. (The selections for sensitivity reports will be grayed
out if there is no feasible solution.) Note that the amount provided column
for the cost row will give the cost.
Use Solver to solve this problem and give sensitivity
analysis. See the videos on the X-Y problem to see how to add in and use
Solver and how to interpret the sensitivity analysis.
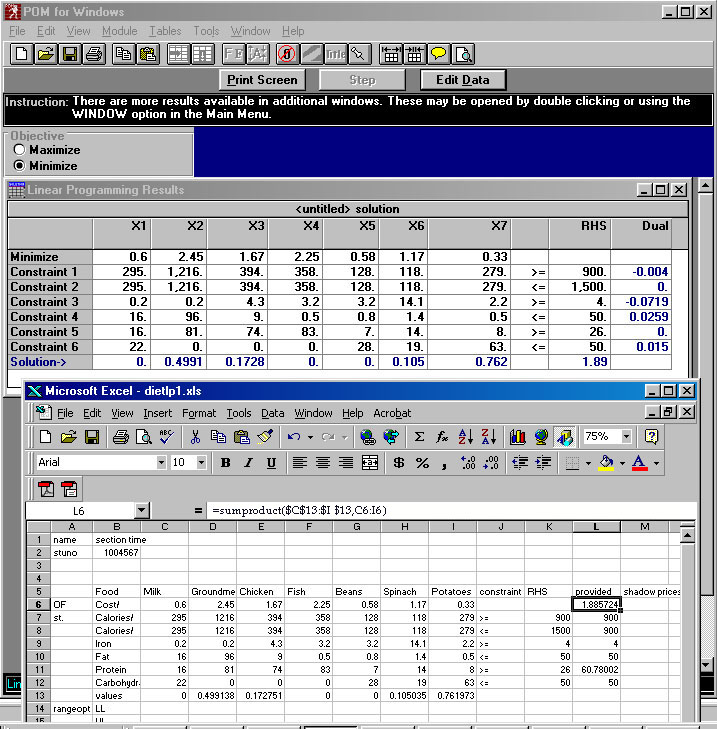
Enter values for the Upper and Lower Limits on the Range of Optimality and the Shadow Prices on this sheet and put it first to facilitate grading. It's easiest to understand these on the POM-QM sensitivity analysis (Ranging) but you should compare these to the SOLVER sensitivity analysis just to understand how they are expressed differently.
Table of Food Values* and Costs
Food Calories/ Iron Fat Protein Carbohydrates Cost/
Item Pound (Mg/Lb) (Gm/Lb) (Gm/Lb) (Gm/Lb) Pound ($)
Milk 295 0.2 16 16 22 0.60
Ground meat 1216 0.2 96 81 0 2.AB
Chicken 394 4.3 9 74 0 1.CD
Fish 358 3.2 0.5 83 0 2.25
Beans 128 3.2 0.8 7 28 0.58
Spinach 118 14.1 1.4 14 19 1.17
Potatoes 279 2.2 0.5 8 63 0.33
Source: C. F. Church and H. N. Church, Bowes and Churchís,
Food Values of Portions Commonly Used, 12th ed. Philadelphia, J. B.
Lippincott, 1975.